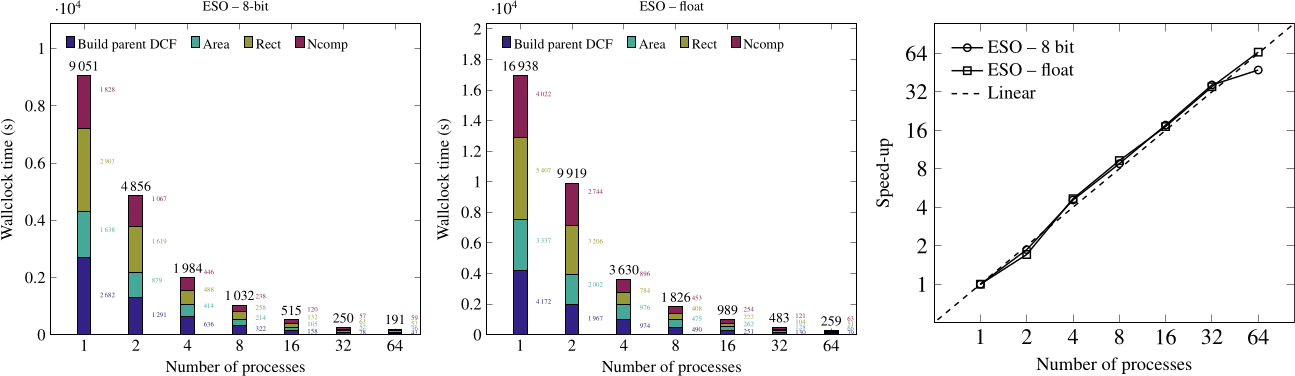Connected operators and component trees are image processing tools used primarily for filtering and simplifying images while preserving important structures. Connected operators act by removing or altering image components based on criteria like size or intensity, without affecting object boundaries. Component trees, on the other hand, are hierarchical structures that represent image regions (or components) at various levels of granularity. They enable efficient analysis and manipulation of the image’s structure, making it easier to apply targeted transformations while retaining meaningful shapes or features in the image. These tools are widely used in areas like computer vision and medical imaging. I have worked on improving certain techniques and deploying a software using them.

Introducing the Connected Component Trees

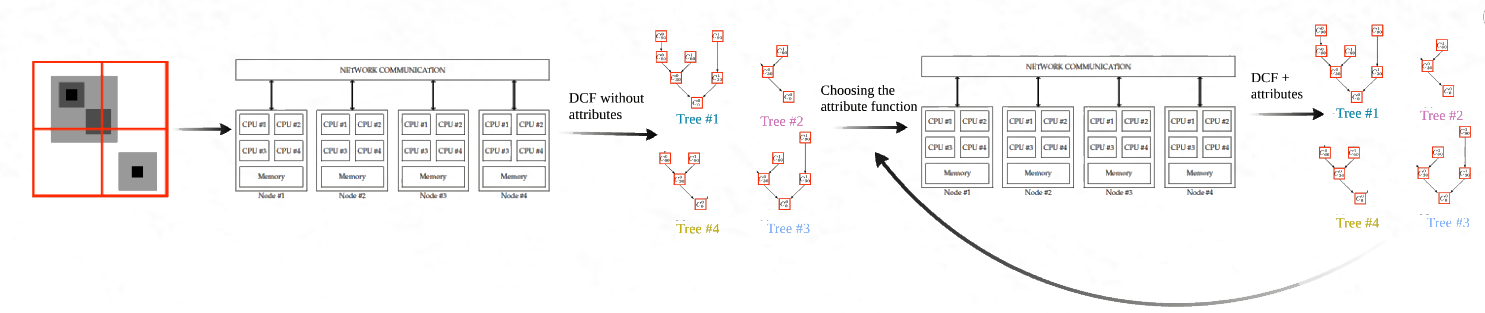
A component tree works by decomposing an image into regions that are connected by pixels sharing similar intensity levels. The tree is built by progressively merging connected components as the intensity threshold changes, resulting in a hierarchical representation where the root of the tree represents the entire image, and the leaves correspond to the smallest connected components at specific intensity levels.

This hierarchical structure allows for a detailed representation of the image’s content at different levels of abstraction. For example, if you consider a grayscale image, a component tree can be built by analyzing the connected regions of pixels at each grayscale intensity level (or threshold). As the threshold increases, new components emerge or merge with existing ones, creating branches and nodes in the tree. Each node in the tree represents a connected component of the image, and the relationships between nodes (parent-child relationships) capture how regions are connected across different intensity thresholds.

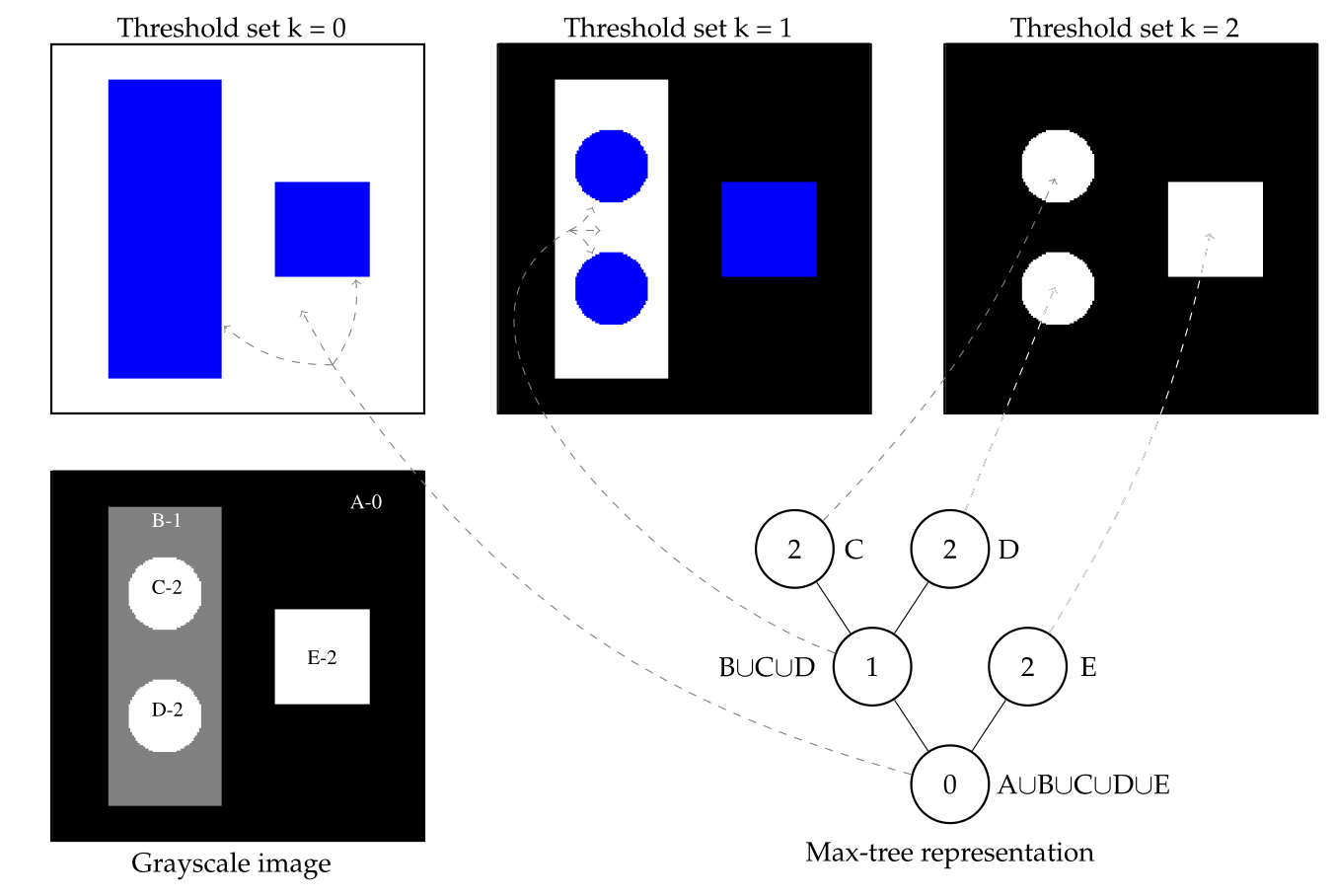
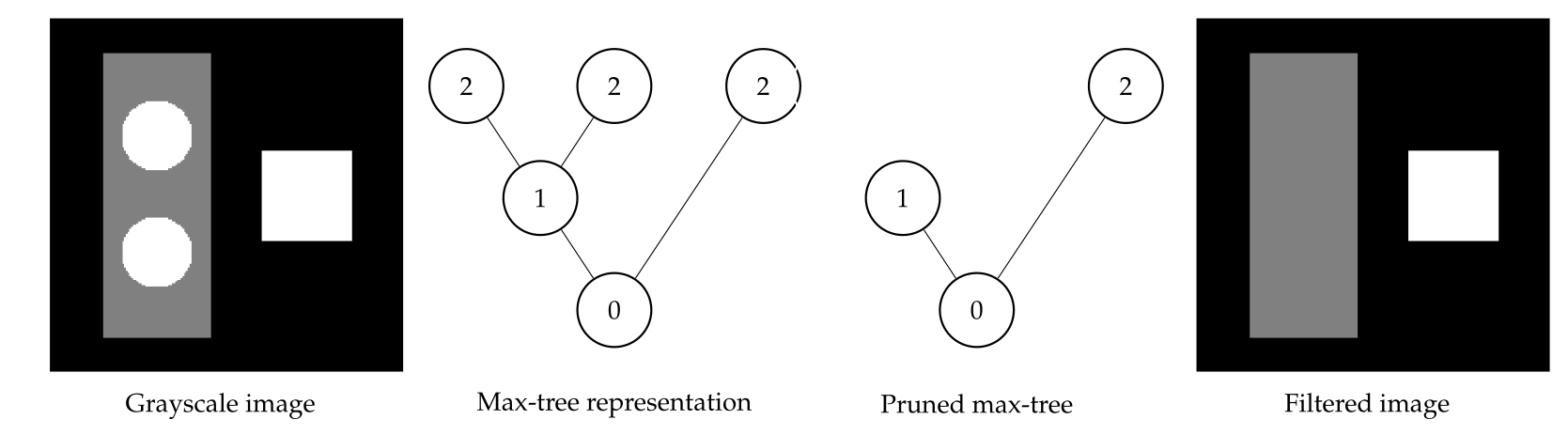
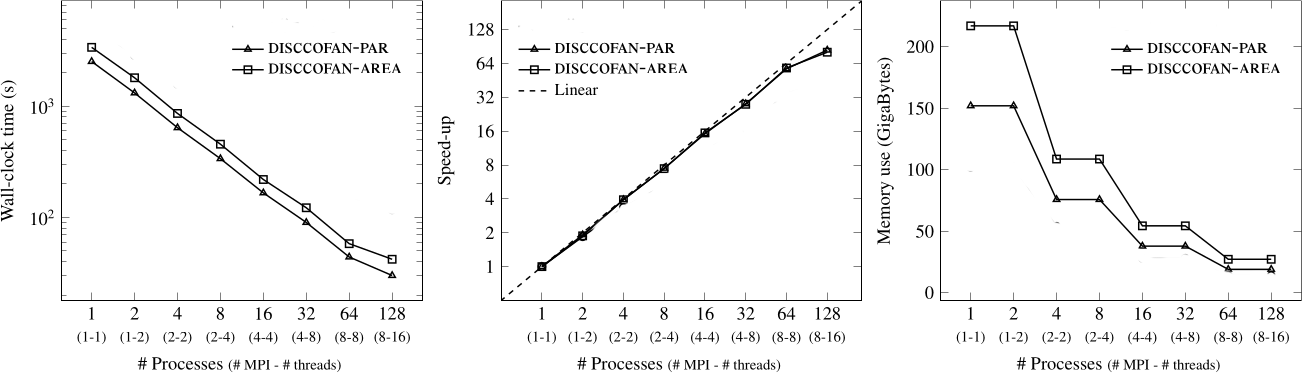
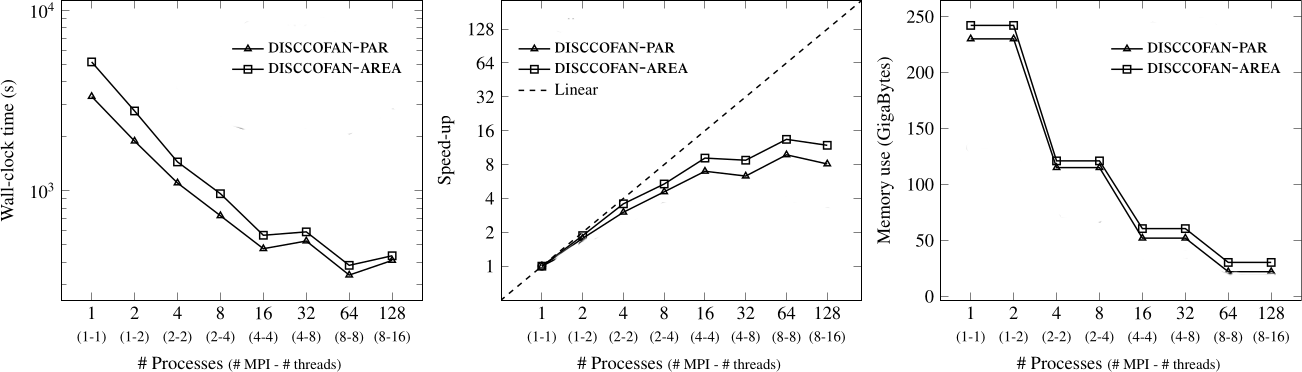
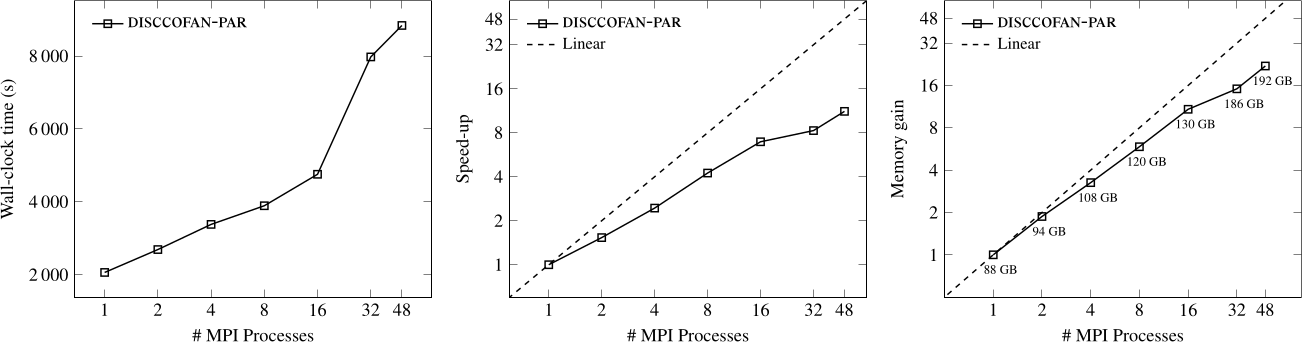
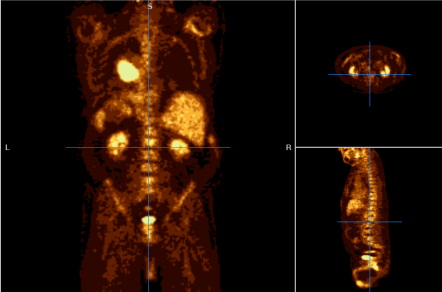
Component trees offer several advantages that make them powerful tools for image analysis. First, they allow for efficient image filtering by manipulating connected components based on their properties, such as size, shape, or intensity. This makes it easy to remove noise, highlight important structures, or simplify the image without distorting object boundaries, which is crucial in fields like medical imaging where object precision is important.

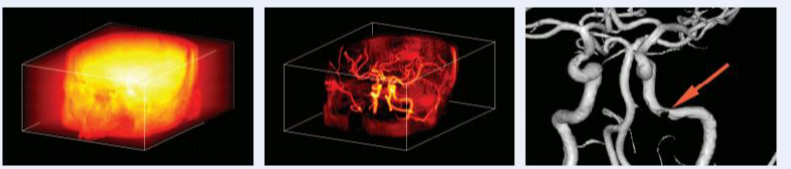
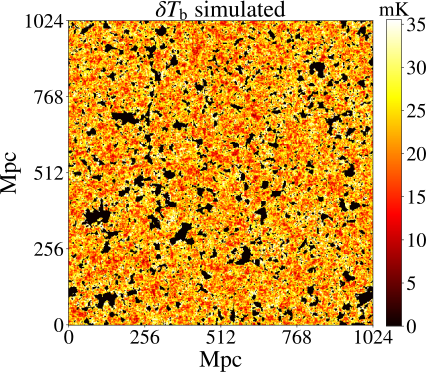
Another fascinating aspect is their ability to represent hierarchical information. Component trees give you a multi-scale view of the image, meaning you can analyze features at different levels of detail, from fine textures to larger regions. This enables adaptive filtering, where you can apply different transformations to various levels of the tree depending on the analysis task. For example, small structures like noise can be easily filtered out, while important large-scale features remain intact. Find some example of applications below

In today's world, we are collecting and generating larger and more detailed images than ever before. Whether it's in medical imaging, satellite data analysis, or astronomical surveys, the size of the images can easily reach into the gigapixel or even terapixel range. Processing these images efficiently is a challenge, especially when working with traditional tools that struggle to handle such huge datasets. This is where the concept of the Distributed Component Forest comes in.

Why Process Very Large Images?

Large-scale images are critical in many fields, from studying the detailed structure of galaxies to diagnosing diseases through medical scans. However, these images come with their own set of challenges, especially when you need to analyze their fine details without losing critical information. For example:

• In medical imaging, high-resolution scans can reveal tiny features that might indicate early signs of disease.
• In astronomy, huge image datasets help scientists explore distant galaxies and phenomena across large areas of the sky.
• Satellite imagery for environmental monitoring requires analyzing vast areas to track climate change, deforestation, or urban development.

To make sense of these enormous images, we need efficient processing techniques that can handle both their size and complexity. Traditional image processing tools simply aren’t enough to tackle such datasets in a timely manner, which brings us to the innovation of Distributed Component Forests.

The Challenge: Processing at Scale

Component trees are a common tool used in image processing. They allow us to break an image down into its connected components — areas of pixels that share similar intensity values. This helps in filtering, segmenting, and analyzing the image’s structure.

However, when dealing with extremely large images, component trees become hard to compute. Building a component tree for a massive image takes significant time and computational resources. This is because traditional methods require the entire image to be processed at once, which can be slow and memory-intensive.

The Solution: Distributed Component Forests

To address this problem, we developed a technique called the Distributed Component Forest. The idea is simple but powerful: instead of processing the entire image as a single component tree, we divide the image into smaller regions. For each region, we build a separate component tree, forming what we call a "forest" of component trees.

This division allows us to process each part of the image in parallel or across multiple machines in a distributed system. Each region is processed independently, but we ensure that the final output is equivalent to processing the entire image as a whole.

This method drastically reduces the time and resources required to analyze large images while maintaining the accuracy of the analysis. Here’s how the process works:

1. Divide the large image into smaller, manageable regions.
2. For each region, build a component tree independently.
3. Exchange information between the individual trees, to ensure that the processing of each individual tree is the same result as if the whole image was processed at once.

Distributed Component Forest

By leveraging parallel and distributed computing, we can process images that were previously too large or time-consuming to handle. This technique opens up new possibilities for real-time analysis and large-scale image processing.

Performance

The Distributed Component Forest technique was implemented as part of the DISCCOFAN code (see Software & Tools) and tested on a high performance cluster at the University of Groningen

Application examples

The code we developed, DISCCOFAN, was featured in applications dealing with large astrophysical data sets, or PET scan of lungs for tumor detections

In short

Distributed Component Forest techniques provide a way to process large images more quickly and with less computational strain, making it a valuable tool for working with huge datasets.

In traditional DCF implementations, after the component trees are built for each subregion of an image, they are used to extract meaningful statistics or attributes from the connected components. These attributes could include size, shape, intensity distributions, or any other region-specific data necessary for image analysis. However, when attributes need to be recalculated for each region, the entire tree often has to be rebuilt.

This constant rebuilding is computationally expensive, especially when dealing with extremely large images. Each rebuild consumes time and resources, slowing down the analysis process and making real-time or large-scale processing more difficult.

Parallel Attribute Computation

To solve this problem, we introduced parallel computation of attributes. Instead of rebuilding the component tree from scratch every time we need new statistics, we use the power of parallel computing to calculate and update the attributes independently.

This means that once the tree is built, it remains intact, and only the statistics or attributes are updated in parallel. By distributing the attribute computation across multiple processing units (such as cores in a CPU cluster), we significantly reduce the time needed for analysis.

Illustrating how this works. You just built a complicated lego. You now decide to make a different structure based on the same set of pieces you just used. The technique we propose enables you to build the new lego you want without having to start from scratch, you start from what you already built and just change the parts that need to be changed.

This improvement makes the Distributed Component Forest approach even more powerful and versatile, paving the way for real-time analysis and larger datasets than previously possible.

Performance evaluation of using parallel attribute computation. A linear scale up of performance is achieved for both low and high dynamic range images. The method was tested with different attribute functions (area, rect, ncomp).

Applications and Impact

This improvement is particularly useful for interactive exploration of data, or using multiple attribute functions on the same data.